Anagram yang dalam bahasa Yunani disebut anagrammatismos mempunyai
arti ana-(up, again, back, new) dan gram (letter). Dalam bahasa
Inggris, anagram sebagai kata benda mempunyai makna yaitu
sebuah kata atau frase baru yang dibentuk dengan menyusun kembali huruf-huruf
dari kata atau frase tersebut. Sebagai contoh dari kata Elvis menjadi
Lives. Sedangkan anagram sebagai kata kerja bermakna yaitu untuk menyusun
kembali huruf-huruf sedemikian rupa.
Anagram adalah salah satu jenis
permainan tebak kata. Objektif permainan anagram adalah menebak kata dengan
huruf-huruf yang telah diacak. Huruf yang tersedia harus dipakai sebanyak jumlahnya.
Contoh yang sederhana, pemain diberikan empat huruf ”upla”, maka pemain harus
menebak kata menggunakan huruf ’u’, ’p’, ’l’, ’a’; dengan tiap huruf tepat
sebanyak jumlahnya. Sehingga kata-kata yang bisa dibentuk adalah ”lupa”,
”palu”, ”pula”, ”luap”, dan seterusnya. Kata yang ditebak harus valid, valid
dalam arti kata tersebut termasuk dalam suatu database yang ditentukan.
Semakin banyak tebakan kata yang benar nilainya semakin baik (Assaat, 2007, hal:1).
Dalam
penelitian yang dilakukan Assaat, 2007 algoritma backtracking dapat
digunakan dalam mencari anagram dari sebuah kata. Pada penelitian tersebut
algoritma backtracking dipakai untuk membangun list kata yang merupakan
kumpulan kata yang dapat disusun oleh huruf-huruf yang telah diacak dan
terdapat di database. Program permainan anagram yang di rancang oleh
Assaat, 2007 melibatkan tiga elemen utama. Pertama adalah pemain, kedua
adalah komputer dalam arti program itu sendiri, dan ketiga adalah database
kata, dimana database tersebut telah terurut secara alfabet.
Secara umum
kerja dari program yang di rancang oleh Assaat, 2007 adalah program melakukan
tiga hal utama, yaitu memilih kata dari database secara acak, membangun
list kata valid dari huruf-huruf kata yang terpilih, dan terakhir mencocokan
string masukan pemain dengan list yang telah dibuat serta dibutuhkan beberapa
data-data tambahan dan fungsi khusus untuk membantu menyelesaikan permasalahan
yang ada.
Data dan fungsi tambahan yang diperlukan
adalah data indeks huruf. Dalam melakukan pencarian apakah string ada atau
tidak dalam database, akan sulit bila setiap pencarian dilakukan dari
awal. Sama seperti halnya menandai halaman awal tiap huruf buku tebal
ensiklopedi dengan jelas agar mudah dicari. Sehingga tiap huruf mempunyai
indeks jumlah kata yang diawalinya. Sebagai contoh, indeks kata yang diawali
huruf ‘d’ yang pertama dalam database adalah 3.325, sehingga pencarian
dimulai dari indeks angka tersebut.
Fungsi tambahan berikutnya adalah fungsi
pembatas indeks, dengan masukan array of karakter, maka fungsi akan
mengembalikan indeks terendah dan tertinggi kata yang masih bisa diawali oleh
masukan karakter tersebut. Sebagai contoh, bila masukan fungsi tersebut adalah
“da” maka fungsi akan mengembalikan indeks pertama dan terakhir kata yang
diawali “da”. Bila tidak ada kata yang bisa dibentuk maka fungsi mengembalikan
angka -99 untuk kedua keluaran. Untuk efektifitas pencarian,angka indeks,
algoritma pencarian yang digunakan adalah binary search agar waktu pencarian
setara untuk setiap huruf.
Skema umum langkah-langkah program
adalah sebagai berikut :
1. Pencarian Kata dan Pengacakan
Program membangun bilangan acak dari angka 1 hingga
[JumlahKataDatabase]. Program akan mengacak indeks huruf dari kata tersebut.
Program mengacak kata dari database, sehingga solusi yang dapat dibentuk
minimal satu buah. Contoh, bila kata yang terpilih adalah “siang”, maka
kata yang bisa dibentuk adalah “siang” itu sendiri, dan “asing”.
2 .
Pembangunan List dari Kata yang Valid
Program akan membangun list kata yang mungkin dan mencocokannya
dengan database. Persoalan telah disederhanakan dengan membatasi jumlah
huruf dalam kata yaitu minimal 4 huruf dan maksimal 8 huruf. (4 <
JumlahHuruf < 8). Kemudian algoritma backtracking dipakai untuk
membangun list kata yang valid, seandainya digunakan algoritma brute force
untuk kasus terburuk dapat kita hitung berapa waktu yang dibutuhkan untuk
membangun list kata yang valid. Misalkan jumlah huruf dari kata yang terpilih
dari database sebanyak delapan, jumlah kata dalam database.
100.000, huruf-huruf dari
kata tersebut hanya dapat membangun kata itu sendiri. Maka kata yang dibangun
sebanyak 8! dan tiap kata harus dicocokkan satu per satu. Bila proses
pencocokan string memakan waktu 1 detik maka, untuk membangun list kata
diperlukan waktu selama 8! x 100.000 = 4.032.000.000 detik. Sedangkan list
hanya akan berisi satu kata, yaitu kata yang diambil dari database.
Sungguh waktu yang lama untuk memulai permainan. Untuk itu di gunakan algoritma
backtracking sebagai penyempurnaan algoritma brute force. Kita
sudah mempunyai data dan fungsi tambahan, yaitu data indeks huruf dan fungsi
batas minimum maksimum. Maka kita akan membangun pohon solusi untuk membangun
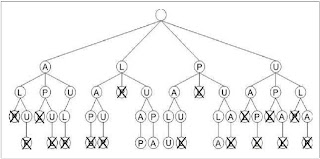
kata-kata yang valid. Sebagai contoh kasus, bila kata yang terpilih dari database
adalah “LUPA”. Maka kata yang dapat dibangun melalui pohon adalah seperti
gambar berikut.
Langkah-langkah dalam
pembangunan pohon adalah sebagai berikut :
1. Simpul dihidupkan sesuai alfabet. Dimulai dari huruf ‘A’. Maka
pencarian langsung dimulai dari indeks huruf A, yaitu 1. Simpul yang dihidupkan
pertama kali oleh simpul ‘A’ adalah simpul ’L’. Maka fungsi pembatas dipanggil
dengan masukkan string “AL”. Karena masih ada kata yang diawali oleh “AL” maka
pencarian diteruskan dengan menghidupkan simpul ‘P’.
2. Fungsi pembatas dipanggil kembali dengan masukan string “ALP”.
Namun fungsi mengembalikan -99 karena tidak ditemukan kata yang diawali “ALP”.
Simpul dibunuh, lalu backtrack ke simpul ‘L’.
Algoritma Backtracking
Salah satu algoritma yang
dapat dipakai untuk mempermudah pencarian anagram suatu kata adalah algoritma backtracking.
Selain algoritma bactracking, pembuatan anagram juga membutuhkan
algoritma string matching yang tepat, karena kata-kata dalam sebuah
anagram harus memiliki makna, dalam hal ini algoritma string matching
yang tepat dapat membantu untuk mencari kata yang dibuat dalam database
kamus yang tersedia, sehingga anagram dapat dibuat dengan lebih cepat dan
efektif.
Algoritma backtracking
pertama kali diperkenalkan oleh D.H. Lehmer pada tahun 1950. Dalam
perkembangannya beberapa ahli seperti RJ Walker, Golomb, dan Baumert menyajikan
uraian umum tentang backtracking dan penerapannya dalam berbagai
persoalan dan aplikasi. Algoritma backtracking (runut balik) merupakan
salah satu metode pemecahan masalah yang termasuk dalam strategi yang berbasis
pencarian pada ruang status. Algoritma backtracking bekerja secara
rekursif dan melakukan pencarian solusi persoalan secara sistematis pada semua
kemungkinan solusi yang ada (Aho, Hopcroft, dan Ullman, 1983, hal:327).
Oleh karena
algoritma ini berbasis pada algoritma Depth-First Search (DFS), maka
pencarian solusi dilakukan dengan menelusuri suatu struktur berbentuk pohon
berakar secara preorder. Proses ini dicirikan dengan ekspansi simpul
terdalam lebih
Algoritma backtracking mempunyai
prinsip dasar kemungkinan solusi. Perbedaan utamanya adalah pada ide dasarnya,
semua solusi dibuat dalam bentuk pohon solusi (pohon ini tentunya berbentuk
abstrak) dan algoritma akan menelusuri pohon tersebut secara DFS sampai
ditemukan solusi yang layak. Nama backtrack didapatkan dari sifat
algoritma ini yang memanfaat karakteristik himpunan solusinya yang sudah disusun
menjadi suatu pohon solusi. Agar lebih jelas bisa dilihat pada pohon solusi
seperti gambar berikut:

Misalkan
pohon diatas menggambarkan solusi dari suatu permasalahan. Untuk mecapai solusi
(5), maka jalan yang ditempuh adalah (1,2,5), demikian juga dengan
solusi-solusi yang lain. Algoritma backtrack akan memeriksa mulai dari
solusi yang pertama yaitu solusi (5). Jika ternyata solusi (5) bukan solusi
yang layak maka algoritma akan melanjutkan ke solusi (6). Jalan yang ditempuh
ke solusi (5) adalah (1,2,5) dan jalan untuk ke solusi (6) adalah (1,2,6).
Kedua solusi ini memiliki jalan awal yang sama yaitu (1,2). Jadi daripada
memeriksa ulang dari (1) kemudian (2) maka hasil (1,2) disimpan dan langsung
memeriksa solusi (6). Pada pohon yang lebih rumit, cara ini akan jauh lebih
efisien daripada brute-force. Pada beberapa kasus, hasil perhitungan
sebelumnya harus disimpan, sedangkan pada kasus yang lainnya tidak perlu.
Penggunaan
terbesar backtrack adalah untuk membuat AI (Artificial Intelligence)
pada board games. Dengan algoritma ini program dapat menghasilkan
pohon sampai dengan kedalaman tertentu dari current status dan
memilih solusi yang akan membuat langkah-langkah yang dapat dilakukan oleh user
akan menghasilkan pohon solusi baru dengan jumlah pilihan langkah terbanyak.
Cara ini dipakai sebagai
AI yang
digunakan untuk dynamic problem solving.
Beberapa kegunaan yang cukup terkenal
dari algoritma backtrack dari suatu masalah “statik” adalah untuk
memecahkan masalah N-Queen problem dan maze solver. N-Queen
problem adalah bagaimana cara meletakkan bidak Queen catur sebanyak N
buah pada papan catur atau pada papan ukuran NxN sedemikian rupa sehingga tidak
ada satu bidakpun yang dapat memangsa bidak lainnya dengan 1 gerakan. Meskipun
mungkin terdapat lebih dari satu solusi untuk masalah ini, tetapi pencarian
semua solusi biasanya tidak terlalu diperlukan, tetapi untuk beberapa kasus
tertentu diperlukan pencarian semua solusi sehingga didapatkan solusi yang
optimal.
Maze
solver adalah bagaimana cara mencari jalan
keluar dari suatu maze (labirin) yang diberikan. Pada maze yang
sederhana dimana field yang dibentuk dapat direpresentasikan dalam bentuk biner
dan pada setiap petak maksimal terdapat 4 kemungkinan: atas, kanan, bawah, dan
kiri. Untuk masalah ini biasanya solusi pertama yang ditemukan bukanlah solusi
yang paling optimal sehingga untuk mendapatkan hasil yang optimal dibutuhkan
pencarian terhadap seluruh kemungkinan solusi. Hal ini disebabkan oleh urutan
pencarian yang telah ditetapkan dalam program apakah menyelidiki kemungkinan ke
arah atas dahulu atau ke arah lainnya dahulu (Putra, Sardjito, Lawrence, 2006,
hal:1).
Algoritma String Matching (Pencocokan String)
Algoritma string matching adalah sebuah algoritma yang
digunakan dalam pencocokkan suatu pola kata tertentu terhadap suatu kalimat
atau teks panjang. Algoritma string matching sendiri dapat dilakukan
dengan beberapa cara tertentu, antara lain cara Brute Force dan cara
Knuth-Morris-Pratt (KMP) (Brassard dan Bratley, 1988, hal:211).
Algoritma-algoritma pencocokan string
dapat diklasifikasikan menjadi tiga bagian menurut arah pencariannya, yaitu :
1) Dari arah yang paling alami, dari kiri ke kanan, yang merupakan
arah untuk membaca, algoritma yang termasuk kategori ini adalah:
a)
Algoritma Brute Force
Cara Brute Force
dilakukan dengan membandingkan seluruh elemen karakter pada pola dengan kalimat
atau teks panjang, dimulai pada elemen karakter pertama pada kalimat tersebut.
Jika tidak sesuai maka pembandingan dimulai dengan elemen kedua dari kalimat
tersebut.
b) Algoritma dari Morris dan Pratt, yang kemudian dikembangkan oleh
Knuth, Morris, dan Pratt
Cara KMP dilakukan dengan
menghitung fungsi pinggiran dari pola terlebih dulu dan kemudian akan dilakukan
perbandingan antara pola dan elemen pertama dari kalimat, jika tidak sesuai,
maka perbandingan tidak dilakukan pada elemen kedua, namun tergantung dari
nilai yang akan dikeluarkan oleh fungsi pinggiran tersebut (Baase, 1988,
hal:213).
2) Dari kanan ke kiri, arah yang biasanya menghasilkan hasil terbaik
secara praktikal, contohnya adalah:
a) Algoritma dari Boyer dan Moore, yang kemudian banyak dikembangkan,
menjadi Algoritma turbo Boyer-Moore, Algoritma tuned Boyer-Moore, dan Algoritma
Zhu-Takaoka
3) Dari arah yang ditentukan secara spesifik oleh algoritma tersebut,
arah ini menghasilkan hasil terbaik secara teoritis, algoritma yang termasuk
kategori ini adalah:
a)
Algoritma Colussi
b)
Algoritma Crochemore-Perrin
sumber : repository.usu.ac.id/bitstream/123456789/20874/.../Chapter%20II.pdf